Première image d’une sphère réduite en 3D : faire entrer la surface de la Terre à l'intérieur d'une balle de ping-pong

Dans les années 1950, Nicolas Kuiper et le prix Nobel John Nash ont démontré l’existence d’une vaste classe d’objets mathématiques paradoxaux tels que des tores plats en 3D ou de sphères réduites, sans pouvoir toutefois les visualiser.
Les sphères, connues pour être rigides, ne peuvent pas être déformées isométriquement (3), c'est-à-dire en préservant les longueurs des courbes, avec une régularité de classe C2. En se basant sur la théorie mathématique de l’intégration convexe (4), les chercheurs sont parvenus à placer une sphère à l'intérieur d'une boule de rayon arbitrairement petit.

Si l'on assimile la surface de la Terre à une sphère ronde, cette théorie permet de réduire son diamètre à celui d'un modèle réduit de globe terrestre ou d'une balle ping-pong tout en préservant les distances géodésiques (5). La surface obtenue, très déformée, se compose de deux calottes sphériques, parfaitement lisses, connectées par une bande équatoriale fortement déformée. Les chercheurs montrent que ce changement de structure géométrique est similaire à celui observé lorsqu'on relie une courbe de von Koch à un segment de droite (voir figure 3). Ces résultats ouvrent des perspectives inédites en mathématiques appliquées, notamment pour la résolution de certaines équations aux dérivées partielles. Les étonnantes propriétés des fractales lisses pourraient également jouer un rôle central dans l'analyse de la géométrie des formes. Leurs résultats ont été publiés dans la revue Foundations of Computational Mathematics, le 6 juillet 2017.




Sphère corruguée et sphère unité
© Projet Hévéa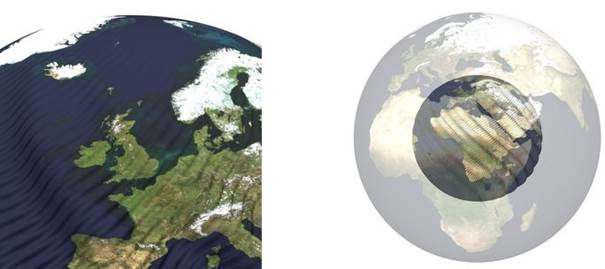



Un globe terrestre isométrique
© Projet Hévéa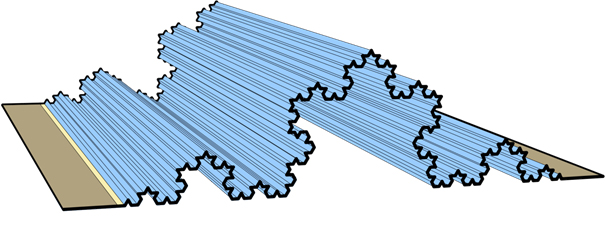



Une surface de Von Koch
© Projet Hévéa

(1) Francis LAZARUS du GIPSA-lab (CNRS/Grenoble-INP/ Université Grenoble Alpes), Vincent BORELLI du laboratoire Jean Kuntzmann (CNRS/Université Grenoble Alpes/Grenoble-INP) et Boris THIBERT de l'Institut Camille Jordan (CNRS/Universités Claude Bernard Lyon 1 et Jean Monnet/Ecole centrale de Lyon/INSA de Lyon)
(2) http://www2.cnrs.fr/presse/communique/2583.htm
(3) Le résultat de John Nash et Nicolas Kuiper montre que ce n'est plus le cas si l'on autorise des déformations moins régulières, de classe C¹.
(4) Utilisée dans la détermination de solutions atypiques d’équations aux dérivées partielles.
(5) Sur le cercle, la distance géodésique est la longueur du plus petit arc de cercle joignant les deux points.
 
Référence : An explicit isometric reduction of the unit sphere into an arbitrarily small ball Evangelis, Bartzos, Vincent Borrelli, Roland Denis, Francis Lazarus, Damien Rohmer, Boris Thibert, Foundations of Computational Mathematics, 6 juillet 2017. DOI :10.1007/s10208-017-9360-1

Pour aller plus loin :
Dossier de presse
Sphère réduite en image

Contact chercheurs :
Francis Lazarus l T. 04 76 82 64 67 l francis.lazarus@gipsa-lab.grenoble-inp.fr  
Vincent Borrelli l T. 04 72.44.79.38 l borrelli@math.univ-lyon1.fr
Boris Thibert l T. 04 57 42 17 84 l boris.thibert@univ-grenoble-alpes.fr